El interés compuesto es aquel que se capitaliza o suma a la deuda, integrando la nueva base sobre la cual se liquidará el interés del periodo siguiente.
Interés.
En economía o finanzas, el interés hace referencia al provecho o utilidad de algo.
Sin embargo, en el contexto del interés compuesto, significa el lucro producido por el capital.
Cuando se invierte el capital o se hace una inversión, el interés es el lucro o ganancia que produce ese capital.
Qué es el interés compuesto.
El interés compuesto es aquel interés que se cobra por un crédito y, al ser liquidado, se acumula al capital (capitalización del interés), por lo que, en la siguiente liquidación de intereses, el interés anterior forma parte del capital o base del cálculo del nuevo interés.
Este sistema, al capitalizar los intereses, hace que el valor que se paga por concepto de intereses se incremente mes a mes, puesto que la base para el cálculo del interés se incrementa cada vez que se liquidan y acumulan los respectivos intereses.
Este sistema es ampliamente aplicado en el sistema financiero. En todos los créditos que realizan los bancos, sin importar su modalidad, se utiliza el interés compuesto.
La razón por la que existe este sistema es porque supone la reinversión de los intereses por parte del prestamista.
Ejemplo de interés compuesto.
A manera de ejemplo, se puede decir que, si se tiene un crédito por $1.000.000 al 2% mensual, al cabo del primer mes se ha generado un interés de $20.000 (1.000.000 * 0.02), valor que se suma al capital inicial, el cual queda en $1.020.000.
Así, en el segundo mes, el interés se calcula sobre $1.020.000, lo que da un interés de $20.400 (1.020.000 * 0.02), valor que se acumula nuevamente al saldo anterior de $1.020.000, quedando el capital en $1.040.400 y así sucesivamente.
Para que no se acumule el interés, es preciso pagar cada mes la totalidad del interés causado, pero si no se paga nada o se paga parcialmente, el valor de los intereses no pagados necesariamente se capitaliza.
Fórmula para calcular el interés compuesto.
El interés compuesto se calcula simplemente aplicando el porcentaje sobre el capital. Por ejemplo, si tenemos un capital de $1.000 y un interés mensual del 5%, tomamos:
1.000 x 0.05 = 50.
Sin embargo, si el interés se capitaliza mes a mes, el asunto se complica porque el capital se incrementará mes a mes, en razón de que el interés compuesto es una función exponencial.
Para determinar el valor futuro de un préstamo a una tasa de interés determinada, en un periodo determinado, se utiliza la siguiente fórmula:
S = P(1 + I)nDe donde:
- S es el valor futuro del crédito, es decir, el valor inicial del crédito más los intereses capitalizados.
- P es el valor presente del crédito, es decir, el valor inicial del crédito.
- I es la tasa de interés expresada en decimales (5% = 0,05 que resulta de 5/100).
- N es el periodo o número de meses de plazo del crédito.
Tomando el ejemplo antes realizado, tenemos:
S es lo que debemos averiguar.
- P = 20.000.000
- I = 3% = 0,03
- N = 2 meses
Entonces:
S = 20.000.000 (1,03)²
S = 20.000.000 * 1,0609
S = 21.218.000.
Es decir que si usted presta $20.000.000 al 3% mensual, en dos meses debe la suma de $21.218.000.
Ahora, si queremos saber únicamente el valor de los intereses, a S le restamos P y tendremos los intereses ganados durante esos dos meses:
21.218.000 (S) – 20.000.000 (P) = 1.218.000 (I).
Interés compuesto en Excel.
Si queremos calcular el interés compuesto en Excel, aplicamos la siguiente fórmula:
=20000000*(1+3%)^2El capital lo podemos reemplazar por la celda donde está, por ejemplo, A1, y quedaría:
=A1*(1+3%)^2Cada variable la podemos incluir en una celda, como por ejemplo:
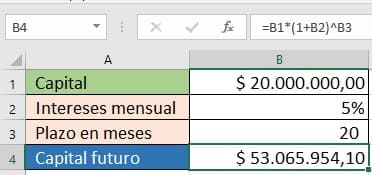
Esta es la fórmula manual llevada a Excel, pero Excel tiene una función específica para ello que es VF, y se puede hacer la tabla de amortización completa con la función PAGOPRIN.
Forma de citar este artículo (APA):
Gerencie.com. (2021, noviembre 10). Interés compuesto [Entrada de blog]. Recuperado de https://www.gerencie.com/interes-compuesto.html
Liquidador de intereses moratorios Dian
¿Se puede repartir la herencia en vida?
Cómo solicitar la prescripción de una deuda en Colombia
Terminación del contrato de arrendamiento
Impugnación de la paternidad
Traslado de régimen pensional
Únete a nuestro canal de WhatsApp para recibir las últimas actualizaciones
Gracias por la página. He realizado varias consultas y he obtenido todas las respuestas solicitadas de manera real y con conocimiento.
Gracias.
Gracias por sus comentarios. Nos alegra saber que ha encontrado útil la información y las herramientas dispuestas para facilitar su consulta.
No me gustó la app.
Lamentamos que la aplicación no haya cumplido con sus expectativas. Su opinión es valiosa para nosotros, y nos gustaría saber qué aspectos específicos no le gustaron o cómo podríamos mejorarla.
¿Cómo calculo el interés compuesto si tengo el valor futuro y el valor actual, pero necesito saber la tasa de cálculo del interés compuesto?
Por ejemplo, tengo $3,500,000 que en 8 meses se triplicó el valor a $10,500,000. ¿Cuál sería la tasa de interés compuesto?
Para calcular la tasa de interés compuesto a partir del valor actual y el valor futuro, se utiliza la siguiente fórmula:
Donde:
En su caso particular tenemos lo siguiente: Valor Actual (VA): 3.500.000 Valor Futuro (VF): 10.500.000 Número de meses o periodos (n): 8 Sustituyendo en la fórmula tenemos: Tasa = ((10,500,000 / 3,500,000) ^(12/8))-1 Tasa = ((3)^1.5)-1 Tasa = 4.2426-1 Tasa=0.42426 Multiplicando por 100 para expresarlo como porcentaje tenemos una tasa aproximada del 42% mensual que redondeamos a dos decimales al 42%.
La profesora Juanita deposita todo el dinero de su jubilación en un banco local. La suma es de 150,000 soles, con una tasa de interés compuesto del 7.5 por ciento anual, capitalizable cuatrimestralmente durante 45 meses. ¿Cuál será el interés que acumulará el dinero de la profesora Juanita?
Para resolver este problema, utilizaremos la fórmula del interés compuesto: M = C (1 + i)^n Donde: – M es el monto total acumulado después de n períodos, incluyendo intereses. – C es el capital inicial o principal (150,000 soles en este caso). – i es la tasa de interés por período. – n es el número total de períodos. Primero debemos determinar cuántos años son 45 meses y luego convertir eso a cuatrimestres para encontrar los periodos correctos. 45 meses equivalen a 3 años y 9 meses (o 3.75 años). Como estamos capitalizando cuatrimestralmente, tenemos que convertir esto a cuatrimestres: \(3 \text{años} * \frac{12}{4} + \frac{9}{4}\) = \(36/4 + 2.25\) = \(36/4 + 9/4\) = \(45/4\) Periodo n será igual a : (150000)*(1+(0.075))^(45/12)=162500 Solución directa utilizando Excel o calculadora financiera sería más rápida como sigue; PV=150000 I=7% N=15 FV=Monto Total=162500
Calcule el monto compuesto que acumulará un capital de $2,500.00 durante 57 meses al 15% anual, con capitalización continua. ¿Me ayudan?
Hola, Juan. Solo debes dividir el interés anual entre 12 para convertir la tasa a mensual. De esa manera, obtienes el resultado esperado.
Buenas noches, muchas gracias por la explicación de las tasas de interés. Es una excelente comunicación con las personas.
Gracias por su comentario. Es nuestro objetivo brindar información clara y precisa, así que nos alegra saber que lo estamos logrando.